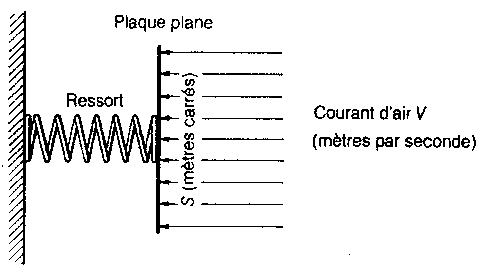
Fig. 2.18 Anémomètre rustique

plaque la rencontre effectivement, en supposant que les particules d'air ne soient pas du tout élastiques, c'est-à-dire qu'elles ne rebondissent pas et qu'elles quittent la plaque en glissant parallèlement à sa surface, et en supposant aussi que rien d'autre ne se produise en arrière de la plaque, nous pouvons dire que le volume d'air qui rencontre la plaque en une seconde est de VS mètres cubes; si r  est la masse volumique, c'est-à-dire la masse d'un mètre cube, la masse d'air qui rencontre la plaque en une seconde est de r VS kg.

La quantité de mouvement de cette masse d'air est r VSxV = r SV².

Par conséquent, la quantité de mouvement perdue par l'air en une seconde est égale à r SV² et, d'après la seconde loi de Newton, la force appliquée sur la plaque est égale à r SV² newtons.

Ainsi, avec toutes ces suppositions, la valeur de K serait de l. Mais si nous avions supposé que l'air était parfaitement élastique et qu'il rebondissait à la même vitesse après avoir rencontré la plaque, le changement de quantité de mouvement de l'air aurait été le double. la force sur la plaque r SV² et K = 2. Dans les deux cas, l'erreur est considérable quand on sait que la valeur de K pour une plaque plane, déterminée par des essais en laboratoire, est d'environ 0,6. L'erreur ne provient pas des principes théoriques concernés, mais de nos suppositions sur ce qui se produit, car elles sont toutes comlpètement fausses! Il est remarquable que la valeur théorique de K soit supérieure à celle trouvée expérimentalement; cela prouve que la plus grande erreur se produit parce qu'on suppose que tout l'air qui s'approche de la plaque la rencontre effectivement et s'immobilise. Les expériences démontrent que la plus grande partie de l'air s'échappe par les bords de la plaque, et l'écoulement devient ensuite turbulent.

Le lecteur se demande sûrement pourquoi on ne se contente pas des faits expérimentaux quand la théorie donne des résultats aussi erronés. La vérité est qu'on s'appuie presque entièrement sur les résultats de l'expérience lorsqu'on étudie les phénomènes aérodynamiques, mais la théorie, comme dans ce cas, donne la nature de la loi et les expériences fournissent les constantes ou les coefficients. Ici, la théorie indique que la force sur la plaque est proportionnelle à r SV², et l'expérience donne l'important coefficient de proportionnalité K.

7 ter - Théorème de Bernoulli
Le théorème de Bernoulli nous propose une autre approche intéressante de ce problème. II nous dit que dans l'écoulement d'un fluide idéal, c'est-à-dire non visqueux, la somme de l'énergie de position (ou énergie potentielle), de l'énergie de mouvement (ou énergie cinétique) et de l'érnergie de pression demeure constante. Dans les cas qui nous concernent, les changements de hauteur du fluide ne sont pas suffisants pour produire un effet appréciable sur le premier terme de cette somme, c'est-à-dire l'énergie potentielle. Par conséquent, la somme des deux premiers termes devrait rester constante; ce qui signifie que si toute l'énergie cinétique est perdue au moment où l'air rencontre la plaque, elle doit être convertie intégralement en énergie de pression.

L'énergie cinétique d'une masse de m kilogrammes se déplaçant à V mètres par seconde est de ½ mV² joules; l'énergie cinétique de 1 m³ d'air est donc de ½ r V² joules. Si toute cette énergie se transforme en énergie de pression, la pression est de ½ r V² pascals et, si la superficie de la plaque est de S mètres carrés, la force totale appliquée sur la plaque sera de ½ r SV² newtons.

Encore une fois, nous remarquons que la théorie indique la nature de la loi, mais nous donne le mauvais coefficient. Dans le présent cas, l'erreur principale vient de ce que nous supposons le fluide non visqueux; la théorie ne tient pas compte des tourbillons formés à l'arrière de la plaque et qui peuvent bien être responsables de l'augmentation de K de ½ (sa valeur théorique) à 0,6 environ (sa valeur expérimentale). Cela est confirmé par le fait que dans un tube de Pitot - nous l'étudierons dans les prochains paragraphes - on obtient en pratique la valeur de K = ½ avec un degré extraordinaire de précision.

8 - La traînée de frottement:
C'est la résistance à l'écoulement que présente une plaque fine et plate parallèle au vent relatif

9 - La traînée de profil:
La traînée de forme et la traînée de frottement constituent une grande partie de la traînée totale d'un avion et la majeure partie dans le domaine des hautes vitesses subsoniques. Parfois, on donne à la somme de ces deux traînées le nom de
traînée de profil, mais nous éviterons ce terme, car il tend à donner l'impression qu'il s'agit là d'une autre appellation de la traînée de forme alors qu'il englobe aussi la traînée de frottement.

10 - La traînée d'onde:
La traînée d'onde et la traînée de couche limite font partie de la traînée de choc. Cette traînée est engendrée par la production d'une onde.

11 - La traînée induite et son calcul:
Toujours dirigée parallèlement au vent relatif. C'est la cause principale des tourbillons de bord de fuite: l'air qui passe sur l'extrados d'une aile tend à s'écouler vers l'intérieur. lI en est ainsi parce que la pression sur l'extrados est plus faible que la pression à l'extérieur des bouts d'ailes. D'autre part, l'air en dessous de l'aile s'écoule vers l'extérieur parce que la pression sur l'intrados est plus grande que celle qui règne à l'extérieur des bouts d'ailes. L'air cherche donc continuellement à contourner les bouts d'ailes, de l'intrados à l'extrados. La façon peut-être d'expliquer pourquoi un allongement élevé est meilleur qu'un allongement faible serait de dire que plus l'allongement est grand, plus la proportion d'air qui s'échappe par les bouts d'ailes est faible. L'air qui contourne les bouts d'ailes n'est plus là pour produire de la portance, c'est ce qu'on appelle parfois une "perte marginale".

Comme les deux écoulements, celui de l'extrados et celui de l'intrados, se rencontrent en bord de fuite sous un certain angle, ils forments des tourbillons qui tournent dans le sens horaire (vus de l'arrière) derrière l'aile gauche et dans le sens anti-horaire derrière l'aile droite. Tous les tourbillons d'un même côté tendent à se rejoindre pour former un seul grand tourbillon qui s'échappe de chaque bout d'aile. Ces deux grands tourbillons s'appellent les tourbillons marginaux.

La plupart des pilotes ont vu ces tourbillons ou, plus précisément, la partie centrale de ceux-ci rendue visible par la condensation. L'humidité de l'air se condense à cause de la chute de pression dans le coeur du tourbillon. Il ne faut pas confondre ces traînées avec la condensation produite par les gaz éjectés des moteurs en haute altitude.

Si l'on considère maintenant le sens de rotation de ces tourbillons, on s'aperçoit qu'il y a un courant d'air vers le haut à l'extérieur de l'envergure des ailes et un courant vers le bas en arrière du bord de fuite. Il ne faut pas confondre ce courant vers le bas avec la déflexion qui se produit normalement. Dans ce dernier cas, la déflexion vers le bas s'accompagne toujours d'une déflexion vers le haut en avant de l'aile si bien que la direction finale de l'écoulement n'est pas modifiée. Mais dans le cas des tourbillons marginaux, la déflexion vers le haut se produit à l'extérieur de l'aile et non pas en avant d'elle, si bien que l'écoulement quittant l'aile est en fin de compte dirigé vers le bas. Par conséquent, la portance, qui agit perpendiculairement à l'écoulement, est légèrement inclinée vers l'arrière et contribue à la traînée. Cette partie de la traînée s'appelle la traînée induite.

Cette traînée induite est inversement proportionnelle au carré de la vitesse, alors que le reste de la traînée est directement proportionnel au carré de la vitesse

Comment calculer le coefficient de la trainée induite (Cxi):
Calculer d'abord l'allongement: envergure/Corde
Calculer ensuite le coefficient de portance (Cz):Cz 1/2 r V².S
Ensuite diviser le coefficient de portance au carré par l'allongement.

Comment calculer la résistance(Rx) en Newtons de la traînée induite:
Multiplier le coefficient de la traînée induite par un 1/2, par la masse volumique de l'air, par la vitesse en mètre secondes au carré et par la surface des ailes.
(Cz²/p A) . 1/2 r V² . S, le résultat est en Newtons
(N= équivalant à la force qui communique à un corps ayant une masse de 1 kilogramme une accélération de 1 mètre par seconde carré).

Comment calculer la puissance requise(en Watts) pour s'opposer à cette traînée induite:
Multiplier la résistance (en Newtons) par la vitesse (mètres secondes) Rx.V .
Il ne reste plus qu'à convertir les Watts en chevaux.
(ch= 736 Watts ou 75 Kilogrammètres par seconde).

12 - La traînée minimale:
On pourrait penser que pour voler à la traînée minimale il suffit de donner à l'avion l'assiette qui lui permette de rencontrer l'air sous son meilleur profil; en d'autres mots, l'assiette qui produise la traînée la plus faible. Mais si l'on y pense bien, on s'aperçois vite qu'une telle idée est erronée. Cette "assiette qui permet de présenter le meilleur profil" implique une vitesse élevée, et nous savons que les effets de la haute vitesse , en ce qui concerne la traînée, annulent les avantages que l'on pourrait gagner en présentant l'avion à l'air dans la bonne assiette. On peut dire que c'est cette assiette qui permet d'atteindre la haute vitesse, et la haute vitesse, en revanche, est cause de traînée. Ce serait faire un trop grand effort pour essayer d'aller vite.

Par ailleurs,il ne faut pas non plus s'imaginer qu'on produirait la traînée la plus faible en volant à la vitesse minimale en palier. En effet, l'aile, à la vitesse minimale, à un angle d'attaque élevé, 15° ou plus, et la traînée induite, pour ne mentionner que celle-là, est extrêmement élevée, il faut alors faire un trop grand effort pour maintenir l'avion dans les airs.

Il doit donc y avoir un compromis entre ces deux extrèmes: ce ne serait pas un avion s'il n'y avait pas moyen de faire un compromis d'une façon ou d'une autre. Ce ne serait pas non plus un avion si la solution n'était pas évidente, à condition qu'on nous montre de quel côté chercher! Etant donné que la portance doit toujours être égale au poids, que nous avons supposé constant et égal à 50 KN, la traînée est au minimum quand le rapport portance/traînée, c'est à dire la finesse, est au maximum. La courbe de finesse fait référence aux profils d'aile seulement. Les valeurs de finesse seront inférieures si l'on considère l'avion dans son ensemble, étant donné que la portance ne sera pas beaucoup plus grande que celle de l'aile seule, alors que la traînée sera considérablement plus élevée, peut-être le double. En outre, les variations de finesse en fonction de l'angle d'attaque, c'est à dire la forme de la courbe, ne seront pas les mêmes pour l'avion complet. Néanmoins, on obtient une valeur maximale, disons 12 à 1, pour un angle d'attaque à peu près identique à celui qui donne la meilleure finesse de l'aile seule (3° ou 4°), et la courbe redescent de chaque côté du maximum, si bien que la finesse est plus petite, c'est à dire la traînée plus grande, si l'on vole à un angle d'attaque plus petit ou plus grand que 4°. En d'autres mots, la finesse diminue si l'on vole à une vitesse plus grande ou plus petite que celle qui correspond à 4°; dans le cas de notre avion, le tableau indique que cette vitesse est de 160 noeuds.

L'angle d'attaque qui donne la meilleure finesse reste le même quels que soient l'altitude et le poids et par conséquent la même distance franchissable. Il s'agit simplement de présenter l'avion à l'air sous le meilleur angle, et cela n'a rien à voir avec la masse volumique de l'air, la charge transportée par l'avion ou même la méthode de propulsion.

Prenons un exemple: 7.600.000 J que nous voudrions obtenir d'un litre de carburant. Le joule étant le travail produit par une force d'un Newton dont le point d'application se déplace d'un mètre, nous pouvons calculer la distance parcourue par l'avion avec un litre de carburant en divisant nos 7.600.000 J par la traînée totale à différentes vitesses. A 100Kts 912 m, à 120Kts 1610 m, à 140Kts 1792 m, à 160Kts 1822 m, à 180Kts 1627 m, à 200Kts 1292 m, de 220Kts 1095 m, 240Kts 912 m, 260Kts 790 m, 280Kts 684 m et à 300Kts 577m seulement. Ces chiffres sont vrais quelle que soit l'altitude. Si le poids est 60 KN au lieu de 50, chaque distance doit être divisée par 60/50, c'est à dire 1,20. Si le poids est inférieur à 50KN, chaque distance sera proportionnellement plus grande.

En résumé, pour obtenir la distance franchissable maximale, il faut voler à un angle d'attaque déterminé, c'est à dire à une vitesse indiquée déterminée. On peut voler à n'importe quelle altitude, mais il faut transporter une charge minimale; quand il faut transporter une charge plus grande, il faut augmenter la vitesse indiquée.

13 - La traînée parasite:
Certains divisent d'une autre façon la traînée totale d'un avion. ils font la distinction entre la traînée de l'aile, c'est à dire la traînée crée par les ailes ou les autres surfaces portantes, et la traînée parasite qui est la traînée des parties qui ne contribuent pas à la portance. Les vieux types d'avion avaient une grande partie de leur traînée totale transformée en traînée parasite.